The Martingale Roulette Strategy
Approximately 250 years ago, the French physicist and philosopher Pascal inadvertently developed an early form of the modern Roulette wheel while trying to create a perpetual motion device. Though he failed, he unintentionally created a consistent money-making tool, particularly for the casinos that own it. However, the question is, is there a reliable way to win at Roulette?
Play at the Best NZ Casinos
Understanding the mathematics behind the game could be the answer. Let’s discuss the Martingale strategy. In a European roulette, there are 18 red spaces, 18 black spaces, and one green space. This arrangement gives the casino a slight edge and is their primary profit source. If you bet on red and the ball lands on a red space, you earn double your stake.
However, if the ball lands on a black or green space, you lose. This is the only type of bet we’ll consider. Given that there are 37 spaces and 18 are red, the success odds are just under 49%, slightly lower than a coin flip. But, could we potentially beat the odds with a strategy to recoup any losses?
| # | Online casino | Casino rating | Welcome | No-deposit | Devices | |
| 1. | 200% up to $1,150 | |
| Play now | ||
| 2. | 100% up to $400 | |
| Play now | ||
| 3. | 100% up to NZ$400 | |
| Play now | ||
| 4. | 200% up to NZ$200 | |
| Play now | ||
| 5. | 100% up to NZ$300 | |
| Play now | ||
| 6. | 200% up to NZ$500 | |
| Play now | ||
| 7. | 125% up to NZ$500 | |
| Play now | ||
| 8. | 100% up to NZ$400 | |
| Play now | ||
| 9. | 100% up to NZ$500 | |
| Play now | ||
| 10. | 100% up to $500 | |
| Play now |
What is the Martingale Strategy?
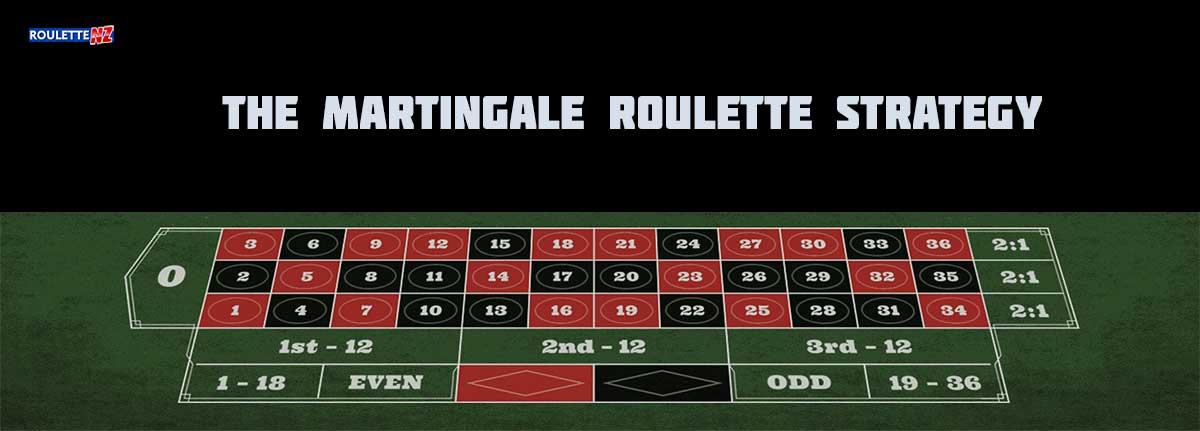
The Martingale strategy, documented before the 18th century, is a betting method that aims to recover any losses and make a small profit. Let’s examine an example where the minimum bet is one dollar. If we win, we bet the same amount again. If we lose, we start the Martingale strategy to recover our losses.
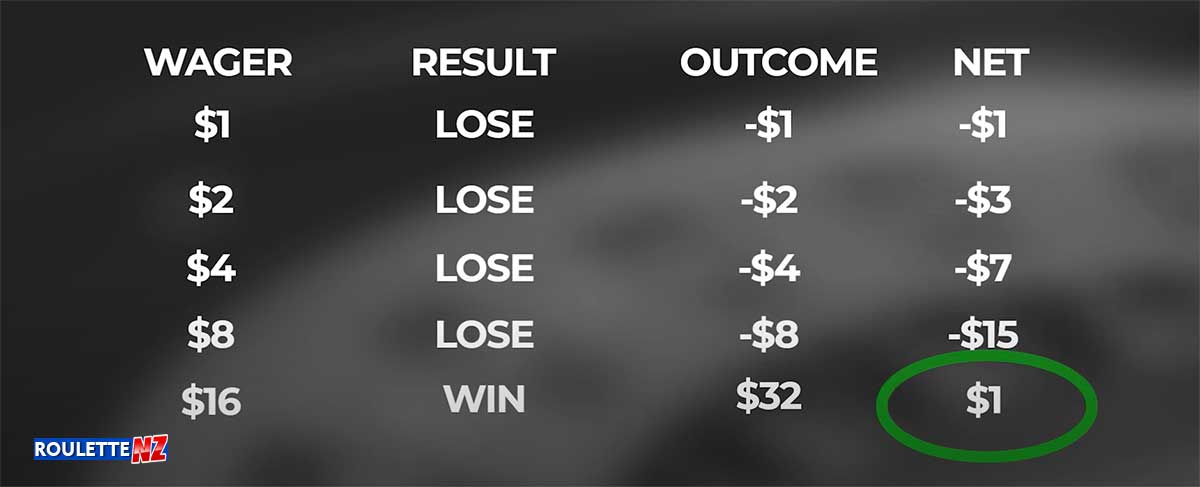
Losing the first bet means we’re down a dollar. To win that back, assuming the winnings are double the bet placed, we need to bet another dollar. If we lose again, our losses increase to $2, and we need to bet $2 to recover. Winning would yield $4, offsetting the previous losses.
If we lose again, we’re down $4. To recover, we must bet $4, hoping to win $8. If we lose, we need to bet $8 to potentially win $16, and so on. Winning at any point during this process would result in a net profit of one dollar.
The pattern is simple: when you win, bet the same minimum amount again. If you lose, start the Martingale strategy – double your previous bet and bet again until you win. Once you’ve won, go back to your initial minimum bet and repeat the process.
However, this strategy seems too good to be true. If it were that simple, casinos would have gone out of business long ago. To understand why this strategy works or fails, we need to delve deeper into the mathematics of optimal stopping problems, which make or break this strategy.
Join Now!
Optimal Stopping Problems
Inspired to develop an anti-aging cream, you, like any good scientist, decide to test whether your “Benjamin Baton” cream can turn back time. You train an AI system to determine people’s ages from photographs by comparing their appearance to their biological age. The test subjects are divided into two groups: one group is given the anti-aging cream, the other a placebo moisturizer.

Initially, you plan to test 225 people in each group and compare the results. After testing all 225 subjects, 47 from the placebo group appear younger, versus 51 from the anti-aging cream group. Given these results, it seems the cream doesn’t work, so you return to the drawing board.
However, upon closer examination of the data, you notice that the results were different when only 132 subjects had been tested. At that point, only 25 people in the placebo group appeared younger, compared to 38 in the anti-aging cream group. A less cautious scientist might have halted the trial then, proclaimed the cream effective, and rushed to market. But you are an ethical scientist.
The key point here is that by selectively choosing when to stop testing, we can influence the results in our favor. This is similar to trying to beat the odds in a casino, but is the opposite of good scientific practice.
So, how do we explain the significant divergence in outcomes between the placebo and the anti-aging cream groups, if there is no real difference? This discrepancy stems from unlikely outcomes being more common than we think, which is also a risk in the Martingale betting strategy. To illustrate this, consider the simpler but analogous situation of flipping a coin: what are the chances of getting five heads in a row?
Join Now!
Breaking Down The Math
A 50% chance occurring five times may intuitively seem like a small probability. This would be 1/2 raised to the fifth power, or about a 3% chance. Interestingly, the odds of obtaining a random sequence of heads and tails is also the same: 3%.

This presents a problem in the Martingale betting strategy, which involves doubling your bet after a loss. This strategy becomes costly very quickly. For instance, after losing a $1 bet, you bet $2. If that bet is lost, you bet $4, then $8, $16, $32, $64, $128, $256, $512, $1,024, and so on. Your financial capacity dictates how long you can endure a losing streak.
Let’s say you have $127. You can withstand seven losses in a row. What’s the chance of that happening if you always bet on tails? This means you can survive seven consecutive heads. The probability of getting seven heads in a row is 1/2 raised to the seventh power, or about 0.8% – less than 1% chance. This seems unlikely, so in theory, it’s safe to play, right?
However, this brings us to the second issue: these seemingly rare events do occur, and much more frequently than you might expect. In a long game, such as an evening of coin flipping, even with a stake of $100, these “seven heads in a row” losses can happen quite regularly. To understand this, we can model it as a Markov chain.
Introduction to Markov Chains
Markov chains are useful for examining the probability of an event occurring based on a history of past events. For example, consider a coin flip. There are two states and a 50/50 chance to either transition between them or remain in the current state. You could flip tails twice, flip heads twice, or alternate between tails and heads.
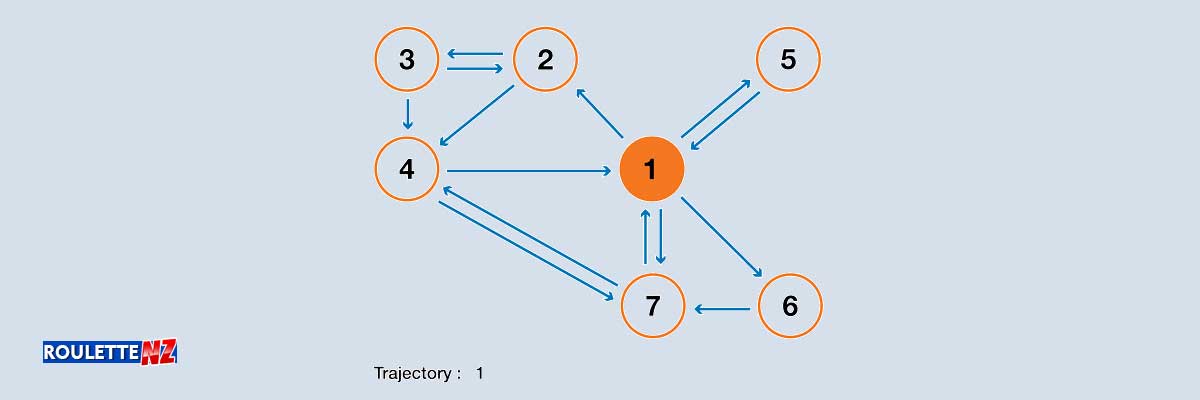
If you want to understand the likelihood of flipping seven heads in a row during an entire night of flipping coins, it might be easier to envision it as a board game. Imagine a board with eight squares labeled from 0 to 7. You start with your marker on square zero and flip a coin. If it’s heads, you move your marker forward. If it’s tails, you return to zero. The game ends when your marker reaches square 7, which is equivalent to flipping tails seven times in a row.
We can represent this process with a transition matrix. We take square ‘n’ as an end state or an absorbing state, and build a matrix that reflects the probabilities of moving from one square to another. Each entry in this matrix represents the probability of transitioning from the state in the leftmost column to the state in the top row.
For instance, the entry in the third row, fourth column represents the probability of moving from two consecutive heads to three, which is 50%. Since there’s a 50% chance of flipping heads or tails at any given flip, there’s always a 50% chance of returning to state zero and starting the process over.
If you make it to stage seven, you win, and the game ends, so the probability there is one. If we raise this matrix to the power of 200, representing 200 coin flips in an evening, and look at the transition from state 0 to 7, we find a probability of around 54%, which means you’re more likely to lose money than win.
This might seem counterintuitive, but it’s borne out by simulation. Using an online calculator to simulate 200 coin flips, it appears that a run of seven heads in a row is quite possible. However, this is all based on the assumption that you can only tolerate seven losses in a row, assuming you had more money.
The Downside of the Martingale Strategy
You could endure more losses, but the required amount of money rapidly escalates. Just over $100 allows you to weather seven losses, while slightly over $1,000 is needed to endure ten losses. To survive an extra 17 losses, you need over $100,000, and over a million is required to survive 20 spins.
The notion of risking a million dollars just to recoup your losses, without making any profit, is rather daunting. But theoretically, it is possible. Why doesn’t the house lose more frequently? Often, the maximum bet you can place is capped.
If you buy in at a dollar, they might cap the maximum spin at $100, which limits the number of losses you can withstand. And, of course, the presence of the green further skews the odds against you. Despite all this, the Martingale strategy can still be effective, albeit not in the long term. If your goal is to win in the short term, it actually works quite well.
How to Use the Martingale Strategy in Real Life Gambling
Consider this scenario: you’ve had a night out, lost your phone, cards, friends, and memory, leaving you with only $14. You need $16 for a taxi ride home. Spotting a casino, you wonder if you should try your luck.
Join Now!
In this case, the math suggests you should. You find a online roulette table, keeping in mind that the green zero space can cause everyone to lose. Placing your bet on red gives you an 18 out of 37 chance, or just below 49% probability, of winning.

Start with a $2 bet. There’s nearly a 49% chance you’ll win immediately, securing your taxi fare. If you lose, bet $4, giving you another chance at winning. If you lose again, bet $8. Either you win the $16 required to go home, or your situation doesn’t worsen significantly.
The odds of losing all three rounds consecutively are approximately 14%. Consequently, the chance of winning is about 86%. In this situation, where long-term gains aren’t the goal, this strategy works well.
These three spins offer an 86% probability that you’ll not only get home but also have an interesting story to tell.
 Jackpot Molly
Jackpot Molly Spinz Casino
Spinz Casino Jonny Jackpot
Jonny Jackpot Casigo Casino
Casigo Casino Skol Casino
Skol Casino Jackpot Village
Jackpot Village Lucky Fox
Lucky Fox Vegas Kings
Vegas Kings Twin Casino
Twin Casino Mummys Gold
Mummys Gold